1. m and n are odd. Show that 2k divides m3 - n3 iff it divides m - n.
2. Let a right angled triangle have side lengths a > b > c. Show that for n > 2, an > bn + cn.
3. Let the vertices of a regular 10-gon be A1, A2, ... , A10 in that order. Show that A1A4 - A1A2 is the radius of the circumcircle.
Solutions
Problem 1
m and n are odd. Show that 2k divides m3 - n3 iff it divides m - n.
Solution
m3 - n3 = (m-n)(m2+mn+n2) = (m-n) x odd.
Problem 2
Let a right angled triangle have side lengths a > b > c. Show that for n > 2, an > bn + cn.
Solution
Induction on n. We have a2 = b2 + c2. Hence a3 = ab2 + ac2 > b3 + c3, so it is true for n = 3. Suppose it is true for n. Then an+1 > abn + acn > bn+1 + cn+1.
Problem 3
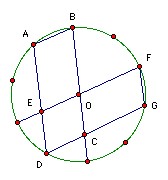
Let the vertices of a regular 10-gon be A1, A2, ... , A10 in that order. Show that A1A4 - A1A2 is the radius of the circumcircle.
Solution
AB is parallel to DG and AD is parallel to BC, so ABCD is a parallelogram. Similarly DEFG is a parallelogram. Obviously BC and EF are (part of) long diagonals and hence intersect at O. Hence DG = EF = EO + EF = AB + radius, which is the required result.
 Labels:
Eötvös Competition Problems
Labels:
Eötvös Competition Problems

 Previous Article
Previous Article
