14th Eötvös Competition Problems 1907

1.  Show that the quadratic x² + 2mx + 2n has no rational roots for odd integers m, n.

2.  Let r be the radius of a circle through three points of a parallelogram. Show that any point inside the parallelogram is a distance ≤ r from at least one of its vertices.

3.  Show that the decimal expansion of a rational number must repeat from some point on. [In other words, if the fractional part of the number is 0.a₁a₂a₃ ... , then a_n+k = a_n for some k > 0 and all n > some n₀.] 

Solutions

Problem 1

Show that the quadratic x² + 2mx + 2n has no rational roots for odd integers m, n.

Solution

The roots are -m±√(m²-2n). If m and n are odd, then m²-2n is 3 mod 4 and hence cannot be a square. Hence the roots are irrational. 

Problem 2

Let r be the radius of a circle through three points of a parallelogram. Show that any point inside the parallelogram is a distance ≤ r from at least one of its vertices.

Solution

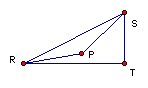
Take the parallelogram to be ABCD. Take r to be the circumradius of ABC. Any point inside the parallelogram lies inside ABC or ADC, which is congruent. Take it to be inside ABC. Then as the diagram shows it must lie inside or on the perimeter of one of the six right-angled triangles with vertex O, each of which has hypoteneuse r. So if is sufficient to show that a point inside or on a right-angled triangle with hypoteneuse r is a distance ≤ r from the vertices at either end of the hypoteneuse.

If P lies on RS, then the result is obvious. Otherwise ∠PRS ≤ ∠TRS and ∠PSR ≤ ∠TSR, so ∠PRS + ∠PSR ≤ ∠TRS + ∠TSR = 90^o. Hence ∠RPS ≥ 90^o, so ∠RPS must be the largest angle of the triangle RPS. Hence PS and PR ≤ RS, which establishes the result. 

Problem 3

Show that the decimal expansion of a rational number must repeat from some point on. [In other words, if the fractional part of the number is 0.a₁a₂a₃ ... , then a_n+k = a_n for some k > 0 and all n > some n₀.]

Solution

We wish to find a/b. We may assume a < b. Carry out the traditional longhand calculation to find a_i: 10a = a₁b + r₁ where 0≤r₁<b, 10r₁ = a₂b + r₂ where 0≤r₂<b, ... ,10r_n = a_n+1b + r_n+1, where 0≤r_n+1<b. If any r_i = 0, then the calculation terminates and only finitely many a_i are non-zero (so a_i becomes periodic with period 1). If not, there are only b-1 possible values for r_i. So we must get a repeat in the first b values, but r_i completely determines all a_j for j > i, so the sequence a_j must become periodic with period ≤ b-1.