2. Let a be an integer, and let p(x1, x2, ... , xn) = ∑1n k xk. Show that the number of integral solutions (x1, x2, ... , xn) to p(x1, x2, ... , xn) = a, with all xi > 0 equals the number of integral solutions (x1, x2, ... , xn) to p(x1, x2, ... , xn) = a - n(n + 1)/2, with all xi ≥ 0.
Solutions
Problem 1
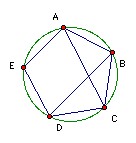
A pentagon inscribed in a circle has equal angles. Show that it has equal sides.
Solution
Consider triangles ABC and DCB. We have ∠ABC = ∠DCB, BC = CB, ∠BAC = ∠CDB (because the pentagon is cyclic). Hence AB = DC. Similarly, AB = DE, BC = ED and BC = EA. So all sides are equal.
Problem 2
Let a be an integer, and let p(x1, x2, ... , xn) = ∑1n k xk. Show that the number of integral solutions (x1, x2, ... , xn) to p(x1, x2, ... , xn) = a, with all xi > 0 equals the number of integral solutions (x1, x2, ... , xn) to p(x1, x2, ... , xn) = a - n(n + 1)/2, with all xi ≥ 0.
Solution
If xi is a positive integral solution to p = a, then xi-1 is a non-negative integral solution to p = a - n(n+1)/2. Conversely if xi is a non-negative integral solution to p = a - n(n+1)/2, then xi+1 is a positive integral solution to p = a. So we have a bijection between the two solution sets.
Problem 3
R is a rectangle. Find the set of all points which are closer to the center of the rectangle than to any vertex.
Solution
The area enclosed by the perpendicular bisectors of OA, OB, OC and OD.
 Labels:
Eötvös Competition Problems
Labels:
Eötvös Competition Problems


 Previous Article
Previous Article
